Euclidean distance matrix completion and point configurations from the minimal spanning tree

Abstract

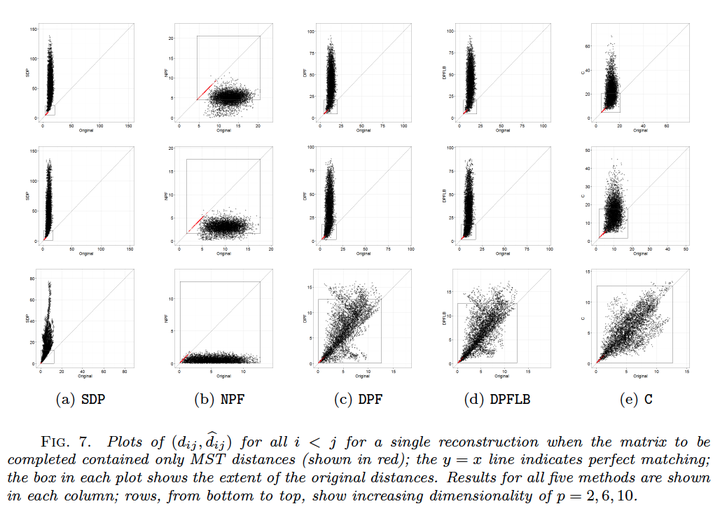
The paper introduces a special case of the Euclidean distance matrix completion problem of interest in statistical data analysis where only the minimal spanning tree distances are given and the matrix completion must preserve the minimal spanning tree. Two solutions are proposed, one an adaptation of a more general method based on a dissimilarity parameterized formulation and the other an entirely novel method which constructs the point configuration directly through a guided random search. These methods as well as three standard edcmp methods are described and compared experimentally on real and synthetic data. It is found that the constructive method given by the guided random search algorithm clearly outperforms all others considered here. Notably, standard methods including the adaptation force peculiar and generally unwanted geometric structure on the point configurations their completions produce.